DSA Binary Search
Binary Search
The Binary Search algorithm retrieves the index of the value it is looking for after searching through an array.
------ IMAGE MUKAVI -----
To learn how the Binary Search algorithm operates, run the simulation.
Try finding value 5 to see what occurs when a value is not found.
Although it requires a sorted array to function, Binary Search is far faster than Linear Search.
Checking the value in the array’s center is how the Binary Search algorithm operates. The value in the left side of the array’s center should be checked next if the goal value is smaller. Because the search region is always half of the previous search area when using this method, the Binary Search algorithm operates incredibly quickly.
The search area is halved in this manner until the array’s search area is empty or the target value is located.
How it works:
1.Examine the value located in the array’s middle.
2.Search the left half of the array if the goal value is less. Search the right half if the goal value is higher.
3.For the newly decreased portion of the array, repeat steps 1 and 2 until the target value is located or the search area is cleared.
4.Return the target value index if the value can be located. Return -1 if the target value cannot be located.
Manual Run Through
To further understand Binary Search before we actually implement it in a programming language, let’s attempt doing the searching manually. We are going to look for value 11.
Step 1: An array is where we begin.
[ 2, 3, 7, 7, 11, 15, 25]
Step 2: Is the value at index 3, in the center of the array, equal to 11?
[ 2, 3, 7, 7, 11, 15, 25]
Step 3: Since seven is less than eleven, we need to look for eleven to the right of index 3. Index 3’s rightmost values are [11, 15, 25]. The middle value 15, at index 5, is the next value to be examined.
[ 2, 3, 7, 7, 11, 15, 25]
Step 4: Since 15 is greater than 11, we have to look past index 5. The only value remaining to check is index 4, as we have already examined indexes 0-3.
[ 2, 3, 7, 7, 11, 15, 25]
We’ve located it!
You can find value 11 at index 4.
Index position 4 is being returned.
Binary Search is now complete.
The following steps can be seen animated by running the simulation:
------ IMAGE MUKAVI -----
Manual Run Through: What Happened?
“Left” and “right” are the algorithm’s initial two variables.
The values “left” and “right” in an array correspond to the index of the first and last values, respectively, at 0 and 6.(left+right)/2=(0+6)/2=3 is the first index used to check if the middle value (7) is equal to the target value (11).7 is lower than the target value 11, so in the next loop the search area must be limited to the right side of the middle value: [ 11, 15, 25], on index 4-6.
To limit the search area and find a new middle value, “left” is updated to index 4, “right” is still 6. 4 and 6 are the indexes for the first and last values in the new search area, the right side of the previous middle value. The new middle value index is (left+right)/2=(4+6)/2=10/2=5.
The new middle value on index 5 is checked: 15 is higher than 11, so if the target value 11 exists in the array it must be on the left side of index 5. The new search area is created by updating “right” from 6 to 4. Now both “left” and “right” is 4, (left+right)/2=(4+4)/2=4, so there is only index 4 left to check. The target value 11 is found at index 4, so index 4 is returned.
Until the target value is located, the Binary Search algorithm generally keeps halving the array search area in this manner.
The target value’s index is returned once the target value has been located. -1 is returned if the target value cannot be located.
Binary Search Implementation
In order to apply the Binary Search algorithm, we require:
1.An array containing values to look up.
2.a desired outcome to look for.
3.a loop that continues to execute if the left index is equal to or less than the right index.
4.An if-statement that returns the index in the event that the target value is found and compares the middle value with the target value.
5.An if-statement that modifies the “left” or “right” variables to limit down the search region if the target value is less than or greater than the middle value.
6.Return -1 at the end of the loop as we now know the target value has not been located.
This is how Binary Search’s generated code appears:
Example
def binarySearch(arr, targetVal):
left = 0
right = len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == targetVal:
return mid
if arr[mid] < targetVal:
left = mid + 1
else:
right = mid - 1
return -1
myArray = [1, 3, 5, 7, 9, 11, 13, 15, 17, 19]
myTarget = 15
result = binarySearch(myArray, myTarget)
if result != -1:
print("Value",myTarget,"found at index", result)
else:
print("Target not found in array.")
Binary Search Time Complexity
See this article for a broad description of time complexity.
See this page for a more comprehensive and in-depth discussion of Insertion Sort time complexity.
The search area is divided in half each time Binary Search evaluates a new value to see if it is the target value.
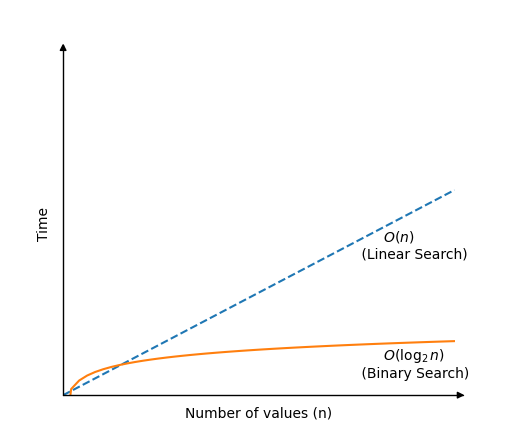
This means that even in the worst case scenario where Binary Search cannot find the target value, it still only needs log2n comparisons to look through a sorted array of n values.
Time complexity for Binary Search is
O(log2n)
Note: When writing time complexity using Big O notation we could also just have written O(logn), but O(log2n) reminds us that the array search area is halved for every new comparison, which is the basic concept of Binary Search, so we will just keep the base 2 indication in this case.
This graph shows how long Binary Search takes, in comparison to Linear Search, to locate a value in an array of n values:
Try the following Binary Search simulation with varying numbers of values (n) in an array to determine the number of comparisons required for Binary Search to discover the desired value:
------ IMAGE MUKAVI -----
As you can see, even with large arrays and missing values, the search only needs to make a small number of comparisons when performing Binary Search simulations.
